Je hebt vast wel eens gehoord van binaire getallen. Ze zijn namelijk belangrijk voor de werking van een computer. Maar weet je ook hoe dit talstelsel werkt? En waarom maakt de computer juist gebruik van dit systeem?
In dit leeslab leren we van alles over bits en bytes. Wat we hier leren kunnen we natuurlijk ook in het echt toepassen, en daarvoor hebben we een lab voor je klaargezet: ‘Bits en bytes met een ledmatrix’. Dit lab kun je dus zelf volgen wanneer je klaar bent!
- Notitie: In dit artikel maken we, voor binaire getallen, gebruik van het veelgebruikte voorvoegsel ‘0b’, zo wordt het getal 1 dus geschreven als 0b1. Met dit voorvoegsel voorkomen we verwarring, want we weten natuurlijk gewoon ’10’ staat voor tien, en ‘0b10’ betekent gewoon twee.
Hoe werkt het binaire systeem?
Binaire getallen zijn goed vergelijkbaar met het systeem wat we dagelijks gebruiken. Er is echter één belangrijk verschil. Het decimaal talstelsel bevat zoals je al weet gewoon tien cijfers, dit zijn 0, 1, 2, 3, enzovoorts. Het binaire stelsel kent maar twee cijfers, en dit zijn 0 en 1.
Toch kunnen we in het binaire stelsel verder tellen dan tot 1. Net als in het decimale stelsel combineren we meerdere cijfers om grotere getallen te maken. Tien, 10, is bijvoorbeeld een samenstelling van 1 en 0, het staat voor het getal wat na 9 komt (9+1=10). In het binaire systeem werkt dit precies hetzelfde, en dat betekent dat het getal wat komt na 0b1 wordt geschreven als 0b10 (0b1+0b1=0b10). Het getal 0b10 is dus het eerst volgende getal na 0b1.
Door telkens meer cijfers toe te voegen kunnen we in het binaire systeem oneindig ver doortellen, net zoals met onze gewone getallen. Met vier tekens komen we bijvoorbeeld al tot 15:
| 0 | 0b0000 |
| 1 | 0b0001 |
| 2 | 0b0010 |
| 3 | 0b0011 |
| 4 | 0b0100 |
| 5 | 0b0101 |
| 6 | 0b0110 |
| 7 | 0b0111 |
| 8 | 0b1000 |
| 9 | 0b1001 |
| 10 | 0b1010 |
| 11 | 0b1011 |
| 12 | 0b1100 |
| 13 | 0b1101 |
| 14 | 0b1110 |
| 15 | 0b1111 |
We zien in deze tabel echter iets vreemds, de getallen bestaan elk uit vier cijfers, bij sommige getallen zijn nullen aan de linkerkant bijgevoegd. Wanneer we werken met decimale getallen doen we dat eigenlijk nooit – het cijfer vijf schrijven we bijvoorbeeld nooit als 005. Maar in het binaire stelsel kan dit ontzettend handig zijn. Dit heeft dan vooral te maken met de werking van bits in de computer.
Bits
Computers maken namelijk gebruik van bits. Geheugenplaatsen, of schakelaars, die alleen aan of uit kunnen staan. Een bit is dan een enkel binair cijfer, en kan dus een 1 of een 0 bevatten.
We kiezen een aantal bits om te gebruiken, en daarmee staat ook vast wat het grootste getal is wat we daarmee kunnen tellen. Met bijvoorbeeld 8 bits kunnen we een getal tussen de 0 en de 255 opslaan. Bij 8 bits kan het getal dan ook nooit groter worden dan 255.
Bytes en data types
Een computer groepeert bits in groepen van acht. Zo een groep heet een byte. Het groeperen verbetert de efficiëntie van de computer. De computer hoeft namelijk niet meer voor elke bit bij te houden waar deze zit, dit doet de computer per byte.
Vanwege deze groepering zal een programmeur er vrijwel altijd voor kiezen om een veelvoud van acht bits voor een getal te reserveren. Dit wordt al voor je geregeld door de programmeertaal die de programmeur gebruikt. De programmeur maakt hiervoor gebruik van datatypes.
Door aan te geven welke datatype je wilt gebruiken, kun je precies bepalen hoeveel bytes de computer zal moeten reserveren. De datatypes ‘byte’ en ‘char’ bevatten bijvoorbeeld maar één byte, een ‘short’ heeft er twee, een ‘int’ bestaat over het algemeen uit vier bytes en een ‘long’ is het grootst, deze heeft meestal acht bytes.
Een datatype geeft echter meer aan dan alleen hoeveel bytes de computer moet reserveren. Er wordt ook aangegeven hoe de data opgeslagen en geïnterpreteerd moet worden. Een gewone short, int en long gebruikt bijvoorbeeld de eerste bit om aan te geven of het getal positief of negatief is. Deze bit behoort dan niet tot het getal. Als programmeur kunnen we deze keuzes wel beïnvloeden. We kunnen deze short, int of long bijvoorbeeld ‘unsigned’ maken om de eerste bit als deel van het positieve getal te gebruiken.
In C++ kan de lengte van de verschillende datatypes af en toe afwijken. Wanneer het belangrijk is om precies aan te geven wat je wilt, dan kiezen we de datatypes int64_t en uint64_t. Het getal in de benaming geeft aan hoeveel bits er gebruikt worden – je hebt de keuze uit 8, 16, 32 en 64. De letter u betekent dan ‘unsigned’.
Voor AVR-boards zoals de Arduino zijn de bytes en shorts altijd de gebruikelijke lengte. Een ”int’ is net als een ‘short 2 bytes lang, en een ‘long’ is 4 bytes lang.
Waarom binaire getallen?
Je vraagt je misschien af: Waarom maken computers gebruik van het binaire systeem?
Dit komt vanwege het belangrijkste component van de computer: de transistor, en zijn voorganger: de vacuümbuis. Een transistor kan (ook) als een digitale schakelaar worden gebruikt: open of dicht. Door de stroomdraad, wat aan de transistor aangesloten is, kan vervolgens wel of geen stroom lopen. Deze toestanden komen goed overeen met de 1 en de 0 van het binaire systeem.
Door de transistoren handig te combineren kunnen eenvoudige berekeningen worden gedaan. We kunnen bijvoorbeeld makkelijk getallen optellen.
Het binaire rekensysteem helpt ons bij het rekenen middels transistoren, en is daarmee belangrijk bij het gebruik van computers.
Bitwise operators
Naast optellen zijn er ook veel andere bewerkingen mogelijk. Dit zijn de bitwise operators. Sommige daarvan zijn makkelijker dan bijvoorbeeld een optelling. Vanwege de eenvoud zijn dit ook de belangrijkste bewerkingen die een computer kan maken. Elke bitwise operator wordt in vrijwel elk programma gebruikt.
NOT (~)
De NOT-bewerking is de meest simpele binaire bewerking welke er bestaat. Je voert één getal in, en er komt één getal uit. De uitkomst is precies het tegenovergestelde van wat je invoert:
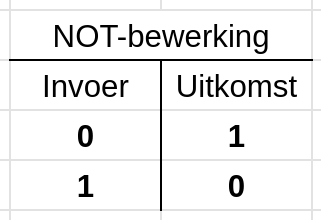
Om een NOT-bewerking aan te geven maken we in computercode gebruik van het ~-teken. De uitkomst van ~0b10100110 is dan 0b01011001. De bewerking wordt voor elke positie afzonderlijk uitgevoerd. Kan je dat in dit voorbeeld zelf nog even controleren?
AND (&)
Om een AND-bewerking uit te voeren hebben we twee getallen nodig. Alleen wanneer beide getallen één zijn is het antwoord een één. Anders is het antwoord een nul. Kijk maar in dit overzicht:
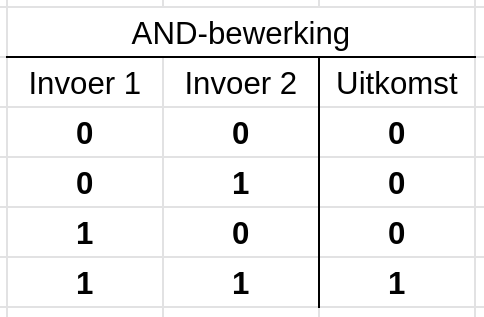
Voor een AND-bewerking wordt het &-symbool gebruikt. De bewerking 0b01010101 & 0b00001111 geeft als resultaat dus het getal 0b00000101.
Ook is de AND-bewerking vanuit een ander oogpunt te bekijken. Wanneer we spreken van ‘bitmasking’ zien we het tweede getal wat we invoeren als een soort masker. In het masker vullen we een één in op de posities waarvan we de waarde willen behouden. Op de posities waarvan we de waarde weg willen gooien vullen we in het masker een nul in. Op de posities van de weggegooide getallen zal in het antwoord altijd een nul komen te staan – kijk maar naar de tabel hierboven.
Wanneer we bijvoorbeeld 0b01010101 invoeren met het masker 0b00001111, zien we dat de eerste vier cijfers gemaskeerd worden. Het resultaat van deze bewerking zal dan 0b00000101 zijn, dat is (0b01010101 & 0b00001111). De gemaskerde cijfers zijn naar een nul veranderd, terwijl de niet-gemaskerde cijfers onaangepast zijn.
OR ( | )
De OR-bewerking lijkt erg op de AND-bewerking. Het verschil is echter dat maar één van de twee ingevoerde getallen een één hoeft te zijn om als uitkomst één te krijgen. Dit zie je in deze tabel:
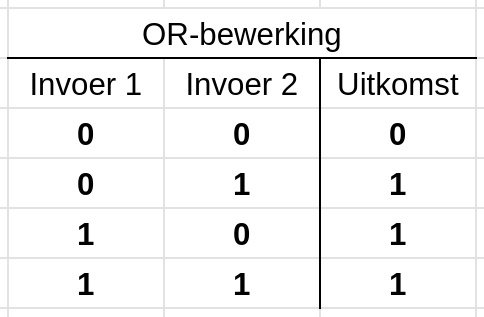
We gebruiken voor de OR-bewerking het |-teken. Dit betekent dan dat de bewerking 0b01010101 | 0b00001111 het getal 0b01011111 als resultaat krijgt.
Net als de AND-bewerking kunnen we ook de OR-bewerking gebruiken om te bitmasken. Echter gebruiken we in het masker een één om aan te geven dat een cijfer gemaskerd moet worden. In het eindresultaat zal het cijfer op deze positie altijd op een één uitkomen. Wanneer we dus bijvoorbeeld het getal 0b01010101 invoeren en het masker 0b11110000 gebruiken zal het resultaat 0b11110101 zijn. We zien dus dat de gemaskerde cijfers veranderen naar een één, de andere getallen blijven onveranderd.
XOR (^)
XOR betekent OR, maar niet AND. Wanneer de bits van elkaar verschillen zal de uitkomst één zijn, anders komt er nul uit. Dit zie je in de volgende:
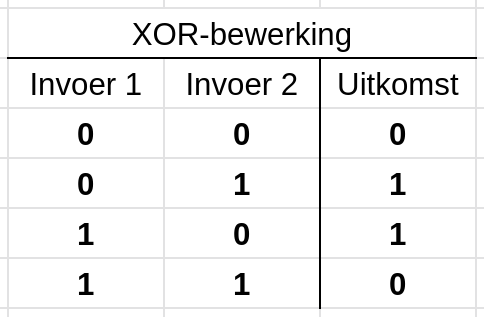
0b01010101 ^ 0b00001111 komt dan uit op 0b01011010.
Ook de XOR-bewerking kunnen we zien vanuit het oogpunt van het bitmasken. De posities waar we in het ‘masker’ een één invullen zullen omkeren (net als een NOT-bewerking). 0b01010101 met het ‘masker’ 0b00001111 zal als resultaat het getal 0b01011010 krijgen. Echter heet dit proces technisch gezien niet bitmasking, de cijfers van het ingevoerde getal hebben op de positie van het masker namelijk alsnog invloed op het resultaat van de bewerking.
Bitshift(<<, >>)
Bitshifting is een heel andere actie. Het eindresultaat van elke losse bit is afhankelijk van zijn buren. Het bitshiften betekent een verplaatsen van alle bits naar links of naar rechts. Bits die van de rand af vallen worden vergeten, en de bits die er aan de andere kant bijkomen zijn dan een nul. Hieronder zien we dit proces in werking:
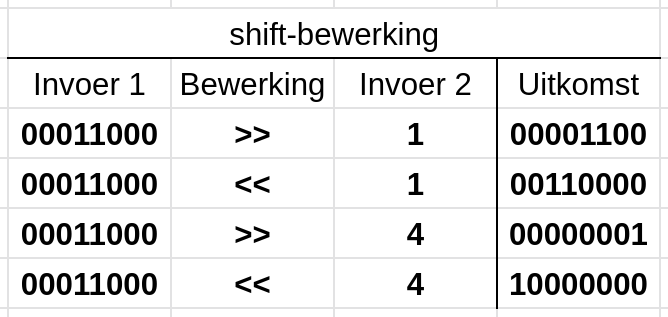
We zien dat het teken ‘<<‘ alle bits naar links verplaatst. De bewerking ‘>>’ verplaatst alle bits naar rechts.
Complexe bewerkingen
Complexe bewerkingen ontstaan door het samenvoegen van de hierboven genoemde eenvoudigere stappen. Op deze manier kunnen we bijvoorbeeld veelgebruikte wiskundige bewerkingen als optellen, aftrekken, vermenigvuldigen en delen uitvoeren.
Computers doen dit voor de veelgebruikte bewerkingen. Dat gebeurt dan niet door de eenvoudigere bewerkingen achter elkaar uit te voeren, maar door de combinatie in hardware in te bouwen. Daardoor worden deze complexe bewerkingen veel sneller uitgevoerd dan wanneer er alleen eenvoudigere opdrachten worden gegeven.
In het echt
Wat we hier geleerd hebben kunnen we natuurlijk ook in het echt toepassen! Hiervoor hebben we een lab voor je klaargezet: ‘Bits en bytes met een ledmatrix’.
